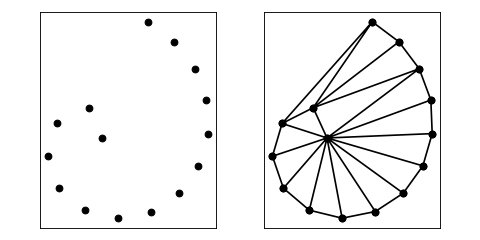
Generating Delaunay Triangulations

Triangle’s default behavior is to find the Delaunay triangulation of a set of vertices. The command below produces the Delaunay triangulation, also illustrated below.

import matplotlib.pyplot as plt

import triangle as tr

spiral = tr.get_data('spiral')
t = tr.triangulate(spiral)

tr.compare(plt, spiral, t)

plt.show()

[py, png, hires.png, pdf]

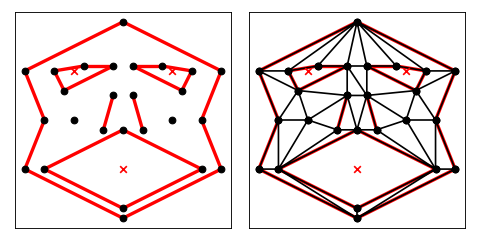
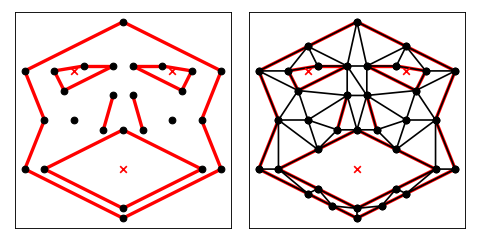
To triangulate a PSLG instead, describe the geometry of the region you wish to mesh in a python dictionary, such as get_data(‘face’), illustrated below. Use the -p switch to specify that the input is a PSLG rather than a vertex set. The command:

trianglulate(get_data('face'), 'p')

will produce the constrained Delaunay triangulation, with holes and concavities removed. (The mouth and eye holes are specified in the input file; the concavities are removed automatically.)

import matplotlib.pyplot as plt

import triangle as tr

face = tr.get_data('face')
t = tr.triangulate(face, 'p')

tr.compare(plt, face, t)
plt.show()

[py, png, hires.png, pdf]

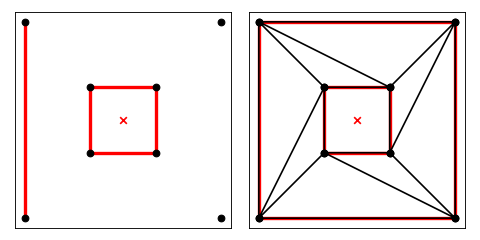
The automatic removal of concavities from the triangulation will be detrimental if you have not taken care to surround the area to be triangulated with segments. In the next example, the input file box.poly defines an open region, so the -c switch must be used to prevent the automatic removal of concavities (which would eliminate the whole triangulation).

trianglulate(get_data('box'), 'pc')

produces the constrained Delaunay triangulation illustrated below. The -c switch causes Triangle to triangulate the convex hull of the PSLG.

import matplotlib.pyplot as plt

import triangle as tr

box = tr.get_data('box')
t = tr.triangulate(box, 'pc')

tr.compare(plt, box, t)
plt.show()

[py, png, hires.png, pdf]

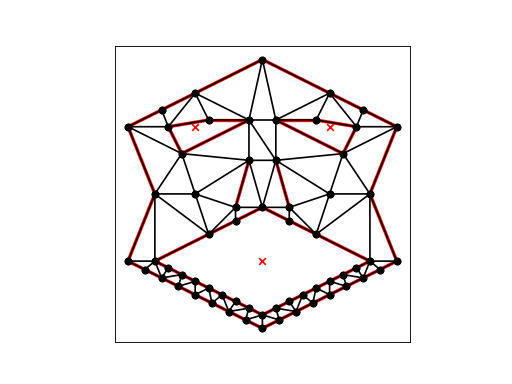
A conforming constrained Delaunay triangulation of a PSLG can be generated by use of the -q, -a, or -u switch, in addition to the -p switch. If you don’t wish to enforce any angle or area constraints, use -q0, which requests quality meshing with a minimum angle of zero. The result is demonstrated below.:

trianglulate(get_data('face'), 'pq10')

import matplotlib.pyplot as plt

import triangle as tr

face = tr.get_data('face')
t = tr.triangulate(face, 'pq10')

tr.compare(plt, face, t)
plt.show()

[py, png, hires.png, pdf]

A conforming Delaunay triangulation of a PSLG can be generated as above, with the addition of the -D switch to ensure that all the triangles of the final mesh are Delaunay (and not just constrained Delaunay).:

trianglulate(get_data('face'), 'pq0D')

import matplotlib.pyplot as plt

import triangle as tr

face = tr.get_data('face')
t = tr.triangulate(face, 'pq0D')
tr.plot(plt.axes(), **t)

plt.show()

[py, png, hires.png, pdf]