API¶
- triangle.triangulate(tri, opts='')¶
Perform triangulation on the input data tri. tri must be a dictionary that contains the following keys:
vertices - 2-D array that stores the xy position of each vertex
segments - optional 2-D array that stores segments. Segments are edges whose presence in the triangulation is enforced (although each segment may be subdivided into smaller edges). Each segment is specified by listing the indices of its two endpoints.
holes - optional 2-D array that stores holes. Holes are specified by identifying a point inside each hole. After the triangulation is formed, Triangle creates holes by eating triangles, spreading out from each hole point until its progress is blocked by PSLG segments; you must be careful to enclose each hole in segments, or your whole triangulation might be eaten away. If the two triangles abutting a segment are eaten, the segment itself is also eaten. Do not place a hole directly on a segment; if you do, Triangle will choose one side of the segment arbitrarily.
regions - optional 2-D array that stores region attributes and areas.
The second (optional) arguments lists the options that should be passed to triangle:
p - Triangulates a Planar Straight Line Graph.
r - Refines a previously generated mesh.
q - Quality mesh generation with no angles smaller than 20 degrees. An alternate minimum angle may be specified after the q.
a - Imposes a maximum triangle area constraint. A fixed area constraint (that applies to every triangle) may be specified after the a, or varying areas may be read from the input dictionary.
c - Encloses the convex hull with segments.
D - Conforming Delaunay: use this switch if you want all triangles in the mesh to be Delaunay, and not just constrained Delaunay; or if you want to ensure that all Voronoi vertices lie within the triangulation.
X - Suppresses exact arithmetic.
S - Specifies the maximum number of added Steiner points.
i - Uses the incremental algorithm for Delaunay triangulation, rather than the divide-and-conquer algorithm.
F - Uses Steven Fortune’s sweepline algorithm for Delaunay triangulation, rather than the divide-and-conquer algorithm.
l - Uses only vertical cuts in the divide-and-conquer algorithm. By default, Triangle uses alternating vertical and horizontal cuts, which usually improve the speed except with vertex sets that are small or short and wide. This switch is primarily of theoretical interest.
s - Specifies that segments should be forced into the triangulation by recursively splitting them at their midpoints, rather than by generating a constrained Delaunay triangulation. Segment splitting is true to Ruppert’s original algorithm, but can create needlessly small triangles. This switch is primarily of theoretical interest.
C - Check the consistency of the final mesh. Uses exact arithmetic for checking, even if the -X switch is used. Useful if you suspect Triangle is buggy.
n - Return neighbor list in dict key ‘neighbors’
e - Return edge list in dict key ‘edges’
>>> v = [[0, 0], [0, 1], [1, 1], [1, 0]] >>> t = triangulate({'vertices': v}, 'a0.2') >>> t['vertices'].tolist() [[0.0, 0.0], [0.0, 1.0], [1.0, 1.0], [1.0, 0.0], [0.5, 0.5], [0.0, 0.5], [0.5, 0.0], [1.0, 0.5], [0.5, 1.0]] >>> t['vertex_markers'].tolist() [[1], [1], [1], [1], [0], [1], [1], [1], [1]] >>> t['triangles'].tolist() [[7, 2, 4], [5, 0, 4], [4, 8, 1], [4, 1, 5], [4, 0, 6], [6, 3, 4], [4, 3, 7], [4, 2, 8]]
(
Source code,png,hires.png,pdf)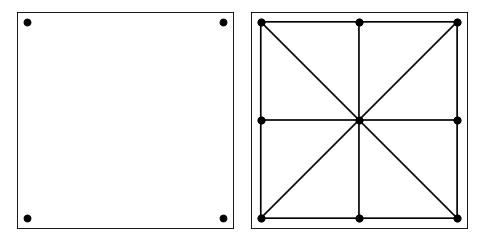
- triangle.convex_hull(pts)¶
Computes the convex hull enclosing pts.
>>> pts = [[0, 0], [0, 1], [1, 1], [1, 0]] >>> segments = convex_hull(pts) >>> segments.tolist() [[3, 0], [2, 3], [1, 2], [0, 1]]
(
Source code,png,hires.png,pdf)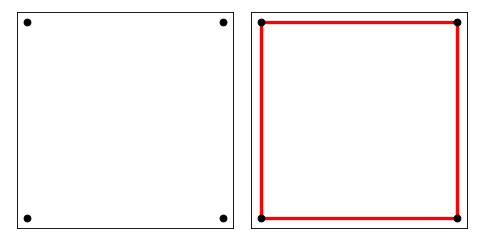
- triangle.delaunay(pts)¶
Computes the delaunay triangulation of points pts.
>>> pts = [[0, 0], [0, 1], [0.5, 0.5], [1, 1], [1, 0]] >>> tri = delaunay(pts) >>> tri.tolist() [[1, 0, 2], [2, 4, 3], [4, 2, 0], [2, 3, 1]]
(
Source code,png,hires.png,pdf)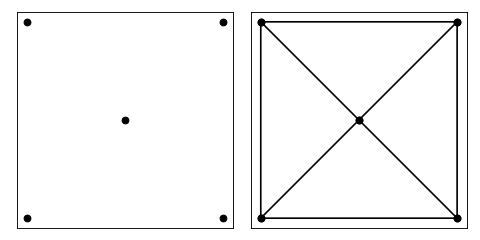
- triangle.voronoi(pts)¶
Computes the voronoi diagram pts.
>>> pts = [[0, 0], [0, 1], [0.5, 0.5], [1, 1], [1, 0]] >>> points, edges, ray_origin, ray_direct = voronoi(pts) >>> points.tolist() [[0.0, 0.5], [1.0, 0.5], [0.5, 0.0], [0.5, 1.0]] >>> edges.tolist() [[0, 2], [0, 3], [1, 2], [1, 3]] >>> ray_origin.tolist() [0, 1, 2, 3] >>> ray_direct.tolist() [[-1.0, 0.0], [1.0, 0.0], [0.0, -1.0], [0.0, 1.0]]
(
Source code,png,hires.png,pdf)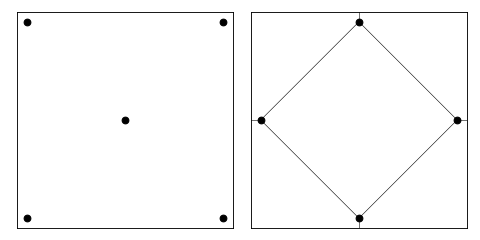
- triangle.get_data(name)¶
Load data samples provided with the module. Examples: A, dots, ell, face, …
- triangle.loads(node=None, ele=None, poly=None, area=None, edge=None, neigh=None)¶
Load a dictionary representing the triangle data from strings.
- triangle.load(directory, name)¶
Load a dictionary representing the triangle data from directory and name.