Definitions (of several geometric terms)¶
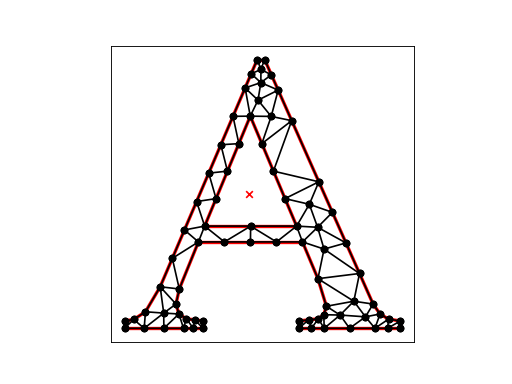
Delaunay Triangulation¶
A Delaunay triangulation of a vertex set is a triangulation of the vertex set with the property that no vertex in the vertex set falls in the interior of the circumcircle (circle that passes through all three vertices) of any triangle in the triangulation.
(Source code, png, hires.png, pdf)
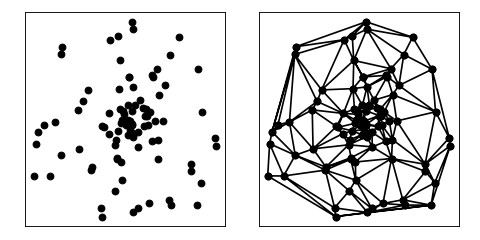
Voronoi Diagram¶
A Voronoi diagram of a vertex set is a subdivision of the plane into polygonal regions (some of which may be infinite), where each region is the set of points in the plane that are closer to some input vertex than to any other input vertex. (The Voronoi diagram is the geometric dual of the Delaunay triangulation.)
(Source code, png, hires.png, pdf)

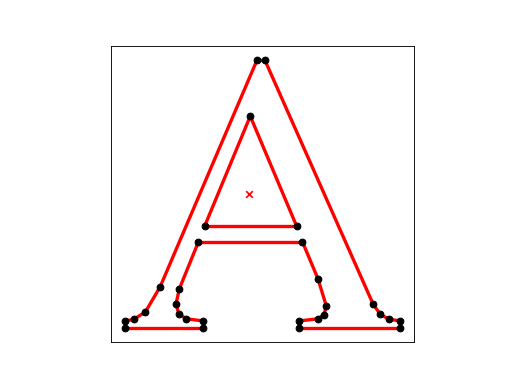
Planar Straight Line Graph¶
A Planar Straight Line Graph (PSLG) is a collection of vertices and segments. Segments are edges whose endpoints are vertices in the PSLG, and whose presence in any mesh generated from the PSLG is enforced.
(Source code, png, hires.png, pdf)
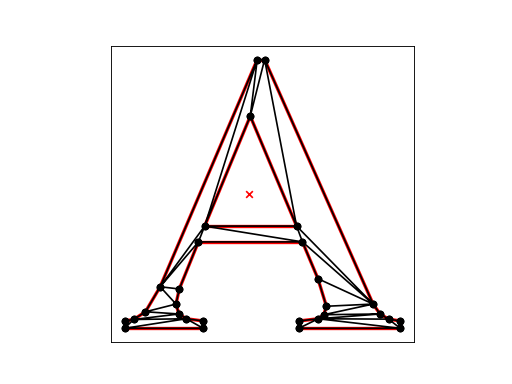
Constrained Delaunay Triangulation¶
A constrained Delaunay triangulation of a PSLG is similar to a Delaunay triangulation, but each PSLG segment is present as a single edge in the triangulation. A constrained Delaunay triangulation is not truly a Delaunay triangulation. Some of its triangles might not be Delaunay, but they are all constrained Delaunay.
(Source code, png, hires.png, pdf)
Conforming Delaunay Triangulation¶
A conforming Delaunay triangulation (CDT) of a PSLG is a true Delaunay triangulation in which each PSLG segment may have been subdivided into several edges by the insertion of additional vertices, called Steiner points. Steiner points are necessary to allow the segments to exist in the mesh while maintaining the Delaunay property. Steiner points are also inserted to meet constraints on the minimum angle and maximum triangle area.
(Source code, png, hires.png, pdf)
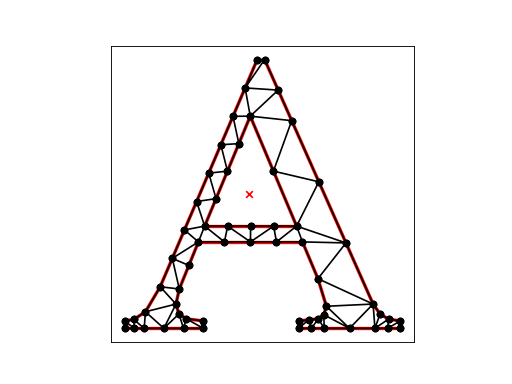
Constrained Conforming Delaunay Triangulation¶
A constrained conforming Delaunay triangulation (CCDT) of a PSLG is a constrained Delaunay triangulation that includes Steiner points. It usually takes fewer vertices to make a good-quality CCDT than a good-quality CDT, because the triangles do not need to be Delaunay (although they still must be constrained Delaunay).
(Source code, png, hires.png, pdf)