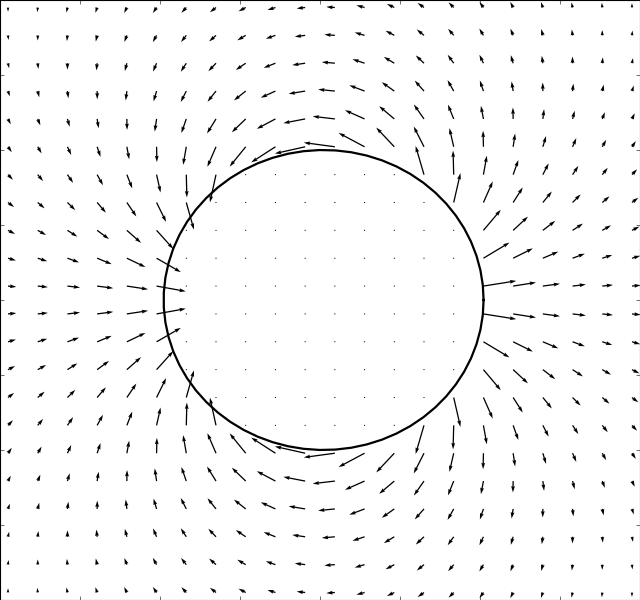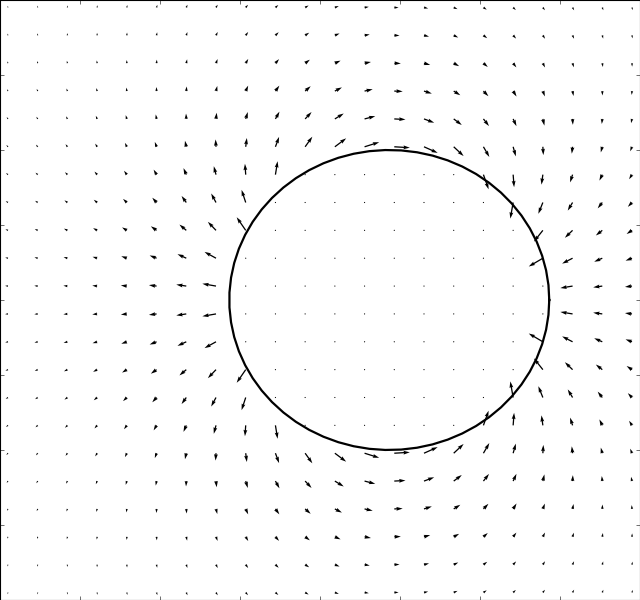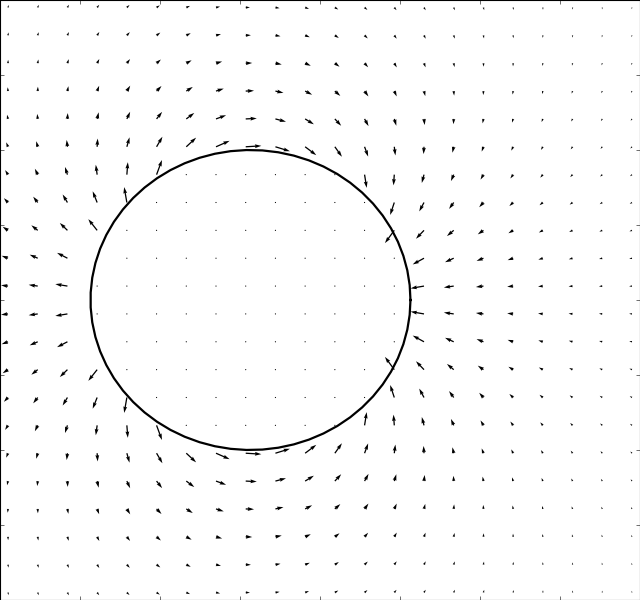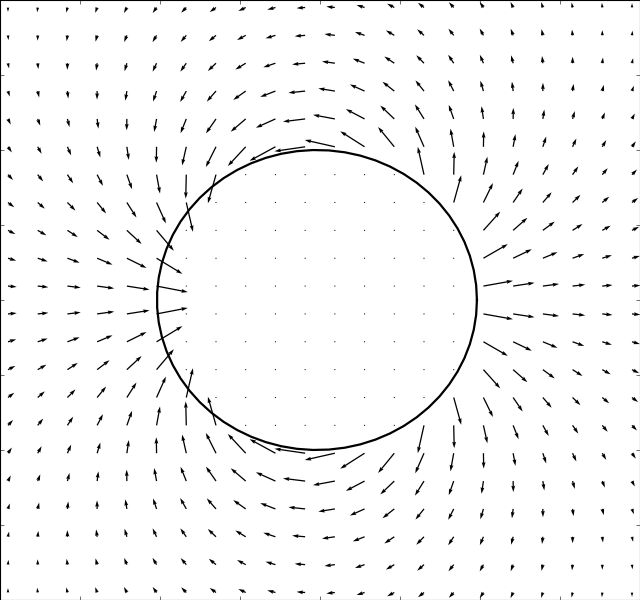
Translating Circle
We now consider the periodic translation of a rigid circle. Its boundary is described by:
with a periodic shape function
The code listing
shapevariables = (
lambda t: 0.5*sin(t),
)
X = lambda s,q: cos(s) + q[0]
Y = lambda s,q: sin(s)
bodies = (
(X,Y),
)
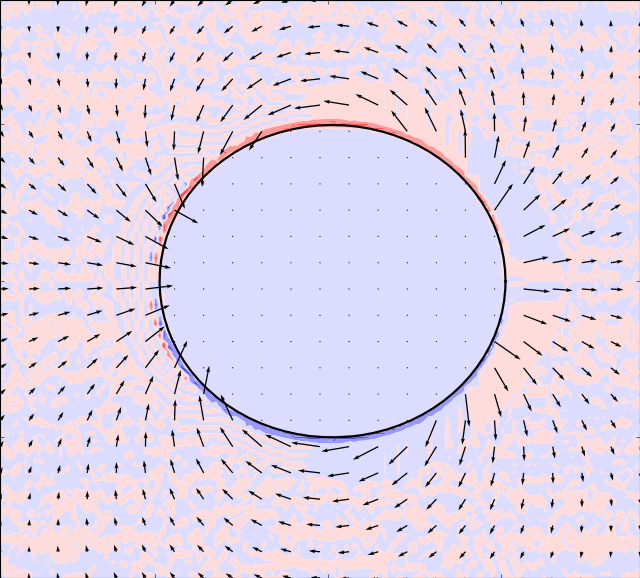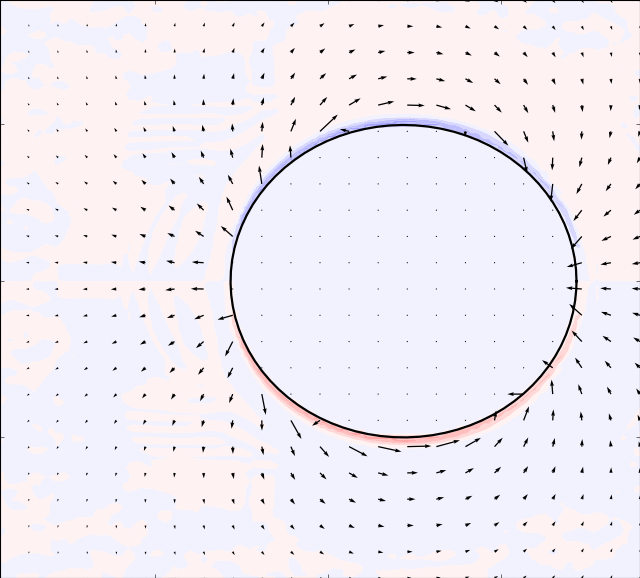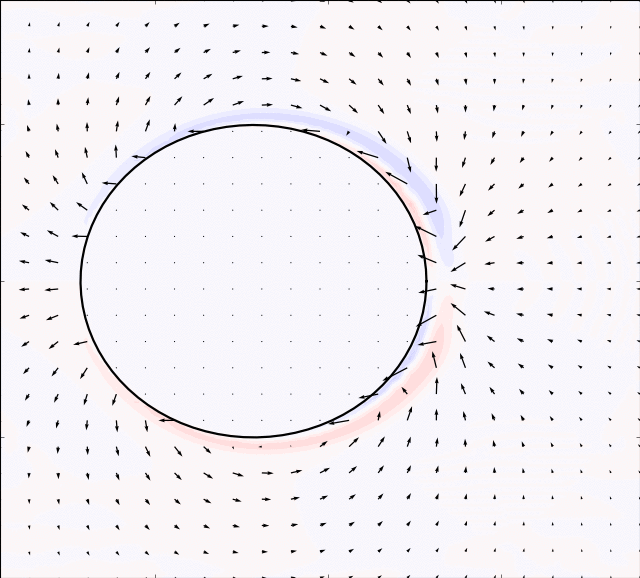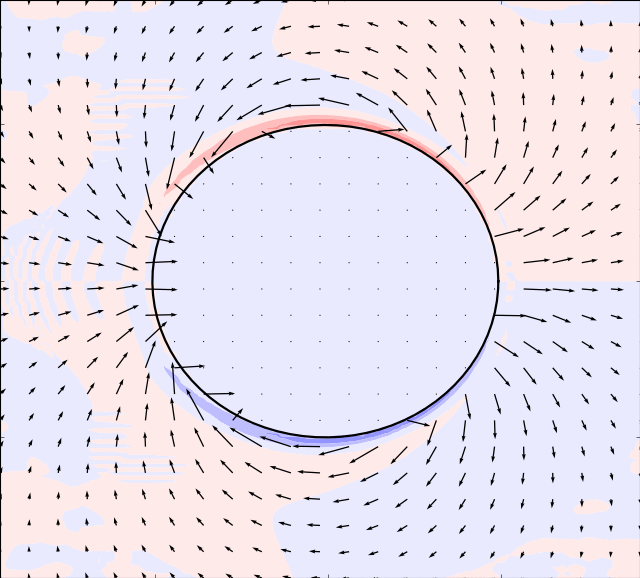
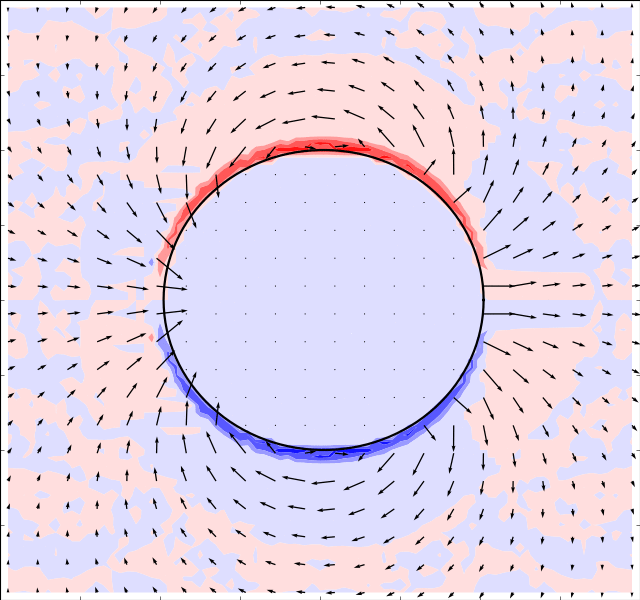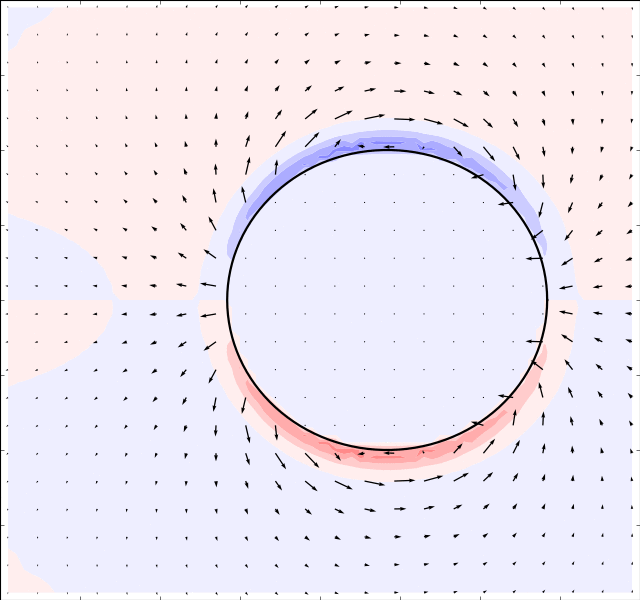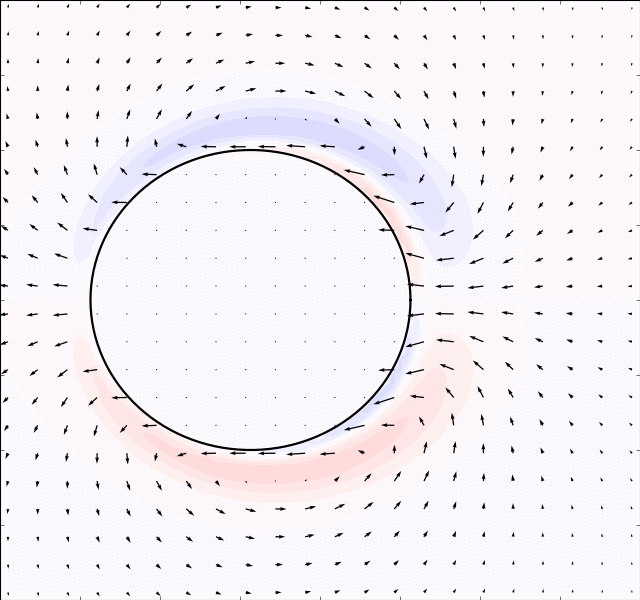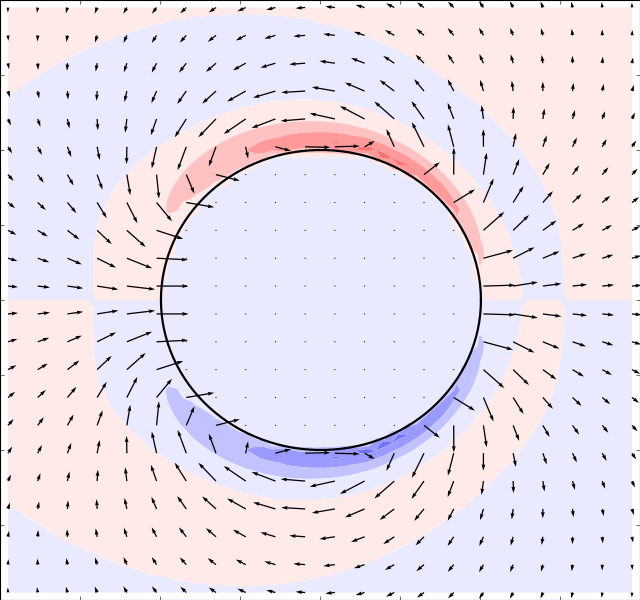
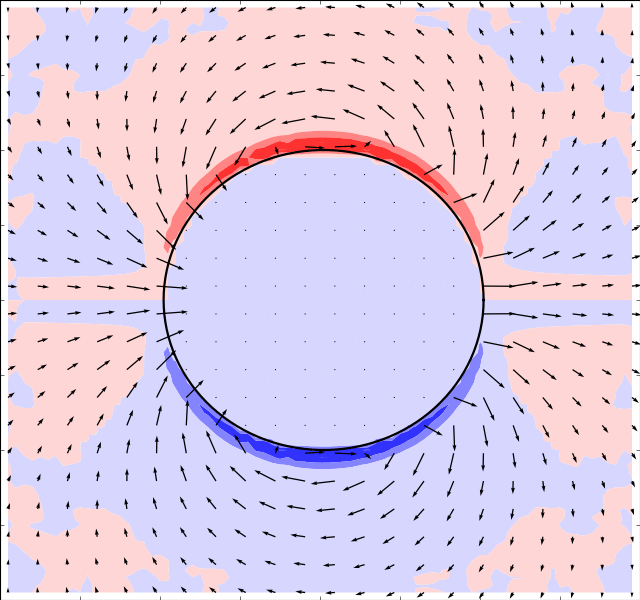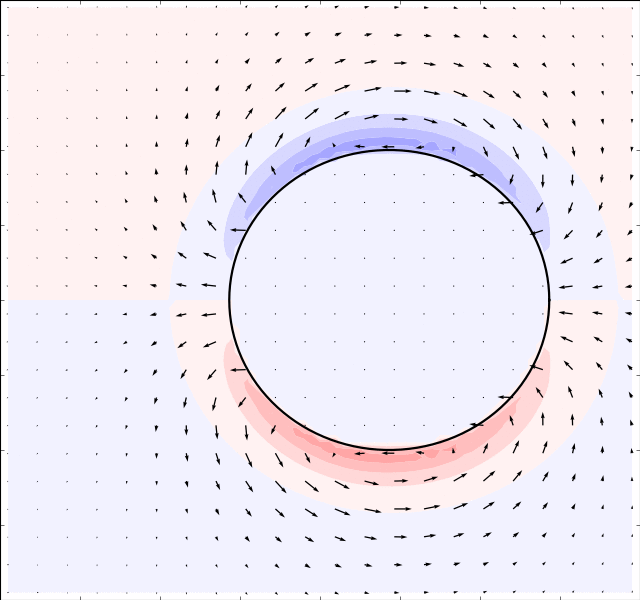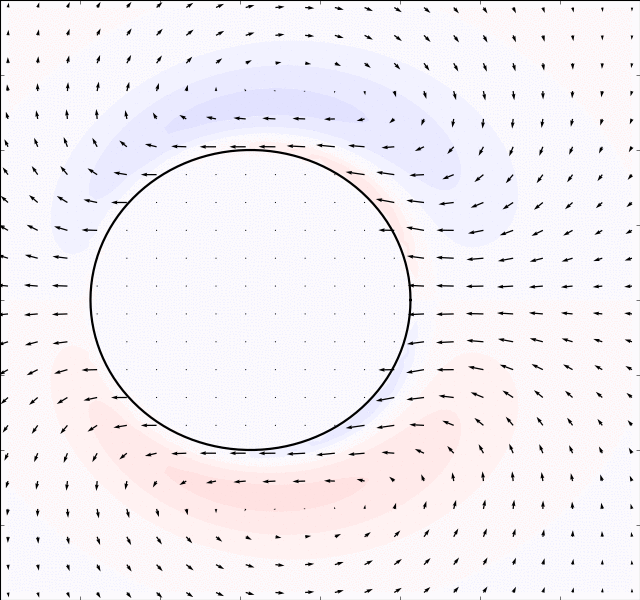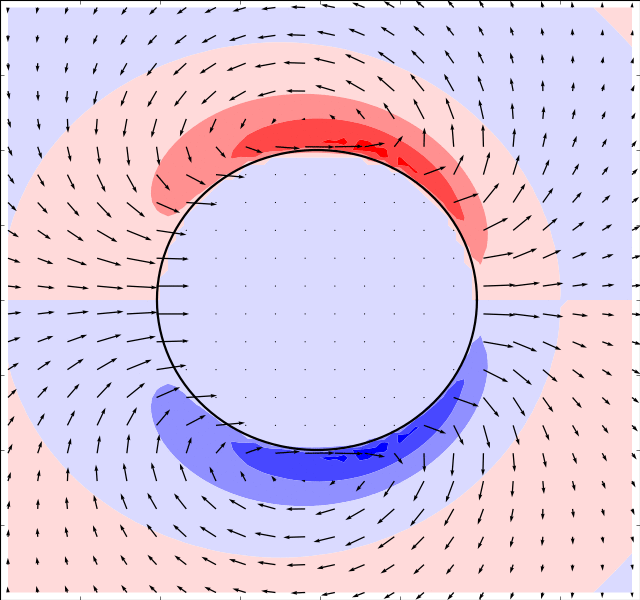
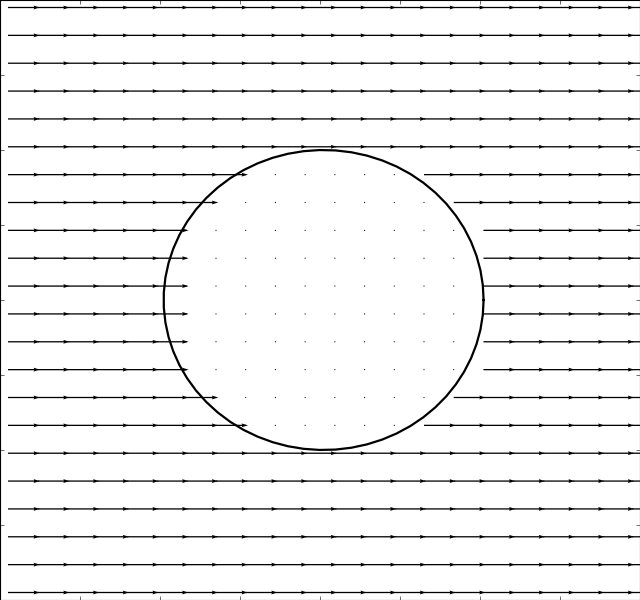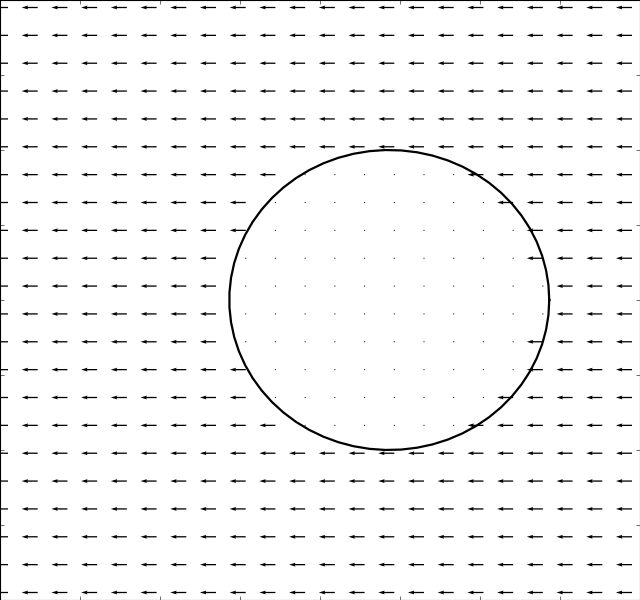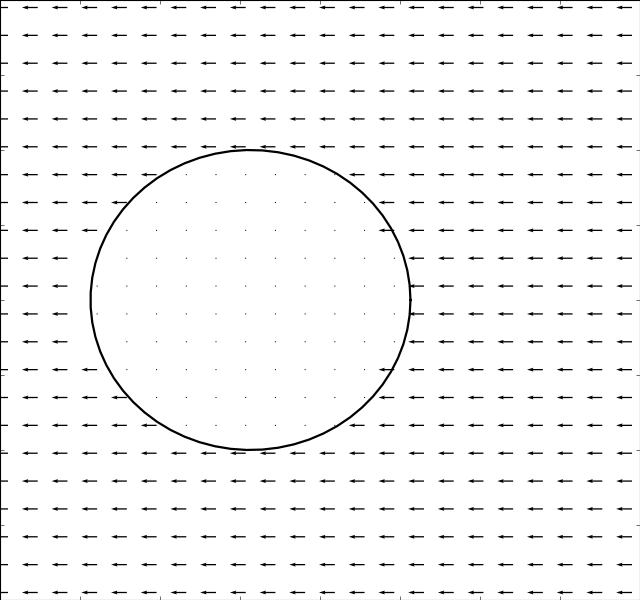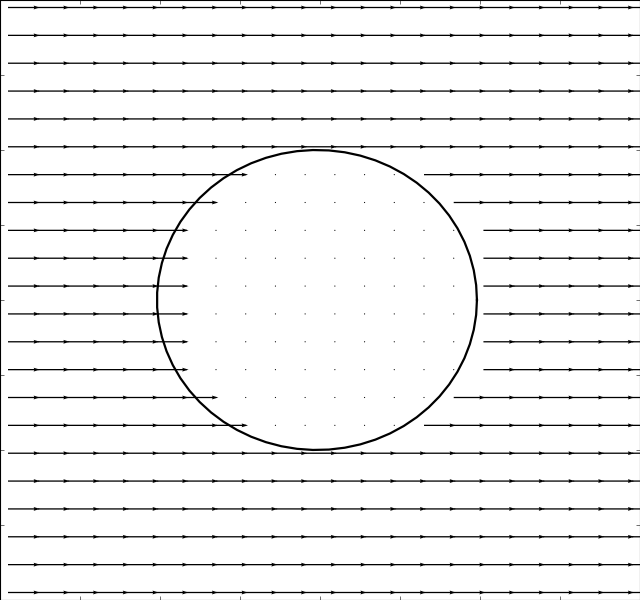
Due to Stoke’s Paradox there does not exist a 2D creeping flow around a translating
cylinder that vanishes at infinity. The Stokesian solver handles this problem
gracefully and outputs a uniform flow for . The immersed boundary method
is used to solve for the
,
and
flows. And
the potential solver (assumes irrotational flow) is used to solve for
. The results are presented in the table below:
There is an inverse correlation between boundary thickness and Reynolds number as expected
Note
You can view the simulations at higher resolution by Right Click->View Image (on Firefox) or using an equivalent method on another browser.