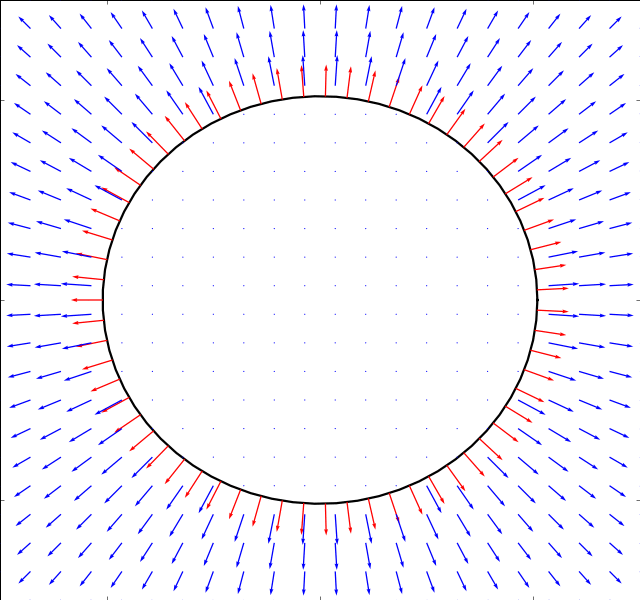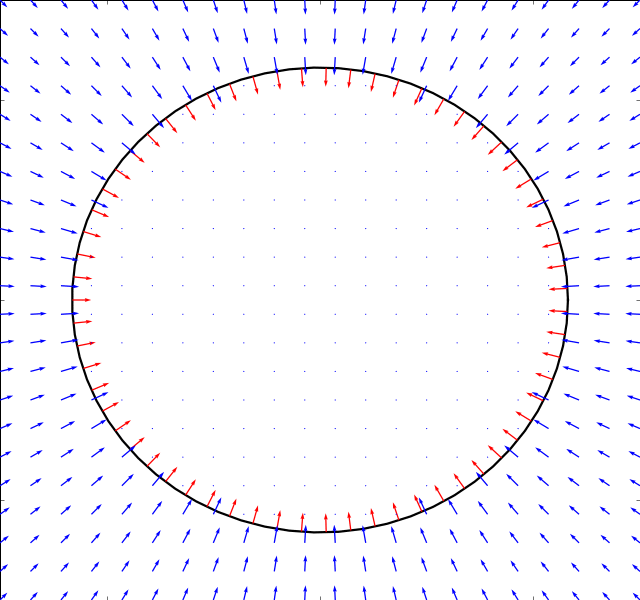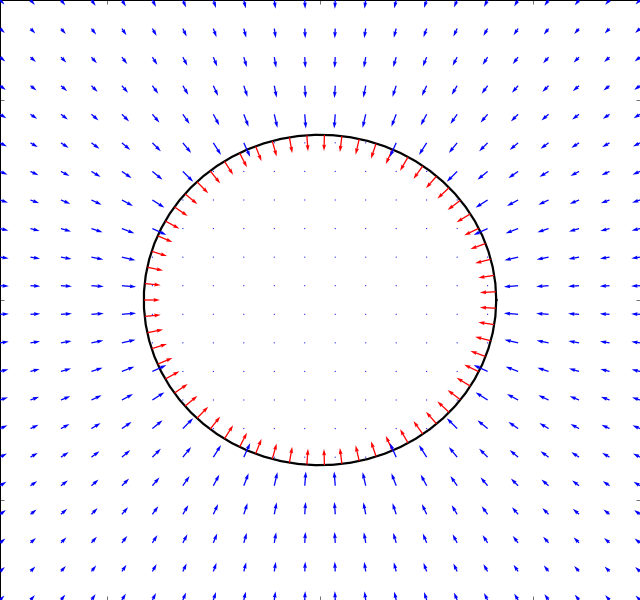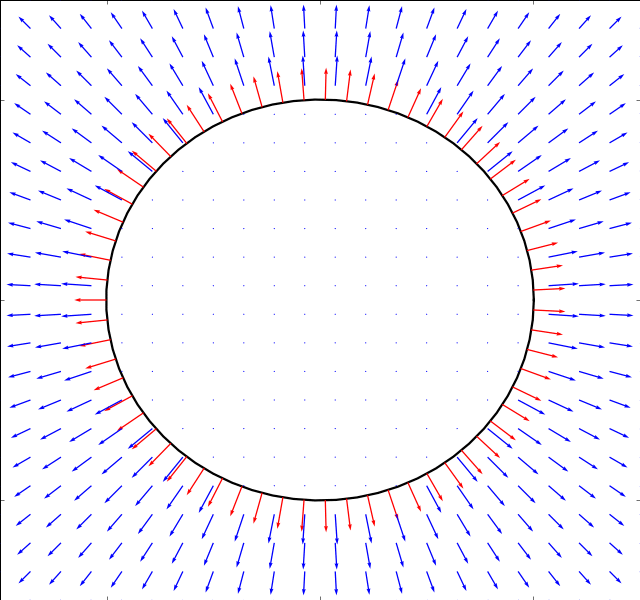
Pulsating Circle
We start with the simple example of a pulsating circle. It’s boundary is described by:
with the periodic shape function
In python code this is expressed as
shapevariables = (
lambda t: sin(t),
)
X = lambda s,q: cos(s) (1+q[0])
Y = lambda s,q: sin(s) (1+q[0])
bodies = (
(X,Y),
)
The solution can easily be found from the continuity equaiton alone
and the numerical simulation is run just for validation purposes. Whereas the panel methods work fine in this case, the immersed boundary method does not converge as it has not been designed to handle cases where the panel size on the boundary changes.
Below is the result of both the stokes and potential solver (the result is the same for both)